[논문 리뷰] NCSN: Generative Modeling by Estimating Gradients of the Data Distribution

paper: Generative Modeling by Estimating Gradients of the Data Distribution (neurips.cc)

 

score-based generative model의 근본 논문이라고 한다.

 

논문을  간략히 요약하면 아래와 같다. 

 

1. 저차원 manifold 문제에서 score가 정의되고, score matching이 가능하도록 다양한 종류의 gaussian noise를 데이터 분포에 추가함으로써 데이터 분포의 gradient를 통한 score matching이 가능하게 한다. 

• generative model을 구현하는데 있어 데이터 분포의 gradient를 근사하는 score function을 학습시키고, Langevin dynamics에서의 MCMC sampling을 활용

 

2. 모든 level의 noise를 추가한 데이터 분포의 gradient를 활용해 score network를 학습시킨 후 annealed Langevin dynamics를 통해 데이터를 sampling한다. 

• sampling 과정에서 활용되는 brownian motion의 hyperparameter인 gaussian distribution의 variance를 고정하는 것이 아니라 geometric sequence를 이루는 순열을 사용해 annealing하는 방법을 사용함 

 

이 방법론은 DDPM과 같은 프레임워크(SDE)에서 설명되어, score-based diffusion을 구성하는 한 축이 된다. 

• DDPM, NCSN 후 DDIM이 나왔다고 보면 된다고 함

 

---

Introduction

기존의 Generative Model은 크게 두 가지로 나뉜다. 

1. Likelihood-based models(우도 기반 모델) - normalizing flow models, VAE 등

• PDF(확률밀도함수)를 직접 학습함. PDF를 정의하고 해당 PDF의 likelihood를 최대화하는 방법
  • 데이터의 distribution 자체를 모델링(데이터의 PDF 자체를 모델링해서 그 PDF로부터 sampling하면 생성이 되는 것) 
• 한계 : 확률의 직접적인 계산이 가능하도록 하기 위해 tractable normaling constant가 보장되어야해서 아키텍처에 대한 제약이 있으며, 실제 데이터의 분포를 모르기 때문에 surrogate objectives(대리 목표)에 의존함 

 

2. Implicit generative models(암시적 생성 모델) - GAN

• 직접적으로 PDF를 모델링하지 않고, Sampling process의 model에 의해 확률 분포를 암시적으로 표현함
• 한계 : 모드 붕괴 등의 문제가 있는 불안정한 적대적 학습 기법에 의존함 -> 학습 불안정 or 성능 떨어짐 

 

이러한 문제를 해결하기 위해 Score-based Generative model은 Score matching과 Langevin Dynamics를 활용한다.  

Score matching으로 훈련된 신경망을 사용해 데이터에서 vector field를 학습하고, Langevin dynamics를 사용해 sample을 생성한다.

 

하지만 이러한 방법도 문제점이 존재한다. 

1. 실제 세계에서의 데이터 세트가 그러하듯, 데이터 분포가 low dimensional manifold에 존재한다면 score는 ambient space에서 정의되지 않고 score matching도 일관된 score 추정치를 제공하는 데 실패한다. 

• score는 데이터 분포의 log gradient라고 생각하면 된다. 

2. low data density 영역에서의 훈련 데이터의 희소성(ex: manifold로부터 멀어진 경우)는 score estimation의 정확도를 방해하고 Langevin dynamics sampling의 mixing을 느리게 한다. 

 

그래서 이 문제들을 해결하기 위해 위 논문에서는 

1. 다양한 크기의 random Gaussian noise를 data에 perturb한다. 

• random noise를 주입함으로 결과 분포가 low dimension manifold에 국한되지 않게 한다.
  • noise의 수준이 크면 원래(unperturbed) 데이터 분포의 low density 영역에 샘플이 생성되어 score estimation이 개선된다.
• 결정적으로 모든 noise level로 조건화된 단일 score network를 학습하고 모든 noise 크기에 대해 score를 추정한다. 

2. annealed version of Langevin dynamics를 제안한다. 

• 처음에는 가장 높은 noise level에 해당하는 score를 사용하고, 점차적으로 원래 데이터 분포와 구별할 수 없을 정도로 작아질 때까지 noise level을 낮추는 an annealed version Langevin dynamics를 제안한다. 

 

이를 통해 제안한 objective는 score network의 모든 파라미터가 tractable하고 어떠한 구조적 제약을 받지 않도록 한다. 

또한 다른 모델들과의 정량적 비교도 가능하다. 

 

Score-based generative modeling(SBGM)

score-based generative modeling의 framework의 두 가지 요소로는 Score-matching, Langevin dynamics가 존재한다. 

Score 

: log-likelihood에 관한 1차 미분

• 이 논문에서는 data density p(x)에 대한 log likelihood의 미분 의미
• s_θ(x)로 표현함
• 파라미터가 아닌 입력 데이터 x에 대한 미분임
• 입력 데이터와 score의 input dimension은 동일해야 함

[논문 Summary] NCSN (2019 NIPS) "Generative Modeling by Estimating Gradients of the data distribution" (tistory.com)

 

• D : a neural network parameterized by θ, which will be trained to approximate the score of p_data(x).
• generative modeling의 목표 : 데이터 세트를 사용해 p_data(x)에서 새로운 samples를 생성하기 위한 모델을 학습하는 것

 

만약 PDF가 아래와 같은 형태로 정의된다고 할 때, normalizing constant Z는 복잡한 적분을 통해서 구해야 하기 때문에 계산이 쉽지 않다.

θ로 parameterize된 energy based model

 

하지만 score function을 이용해 log-likelihood를 계산한다고 하면, log-likelihood에 대해 미분을 취하기 때문에 아래 식과 같이 input에 independent한 normalizing constant 부분이 날아가고 계산이 더 쉬워진다.

 

score network 

논문에서는 Denoising score matching을 이용해 score network를 학습한다.

• input : 데이터(x˜) / output: 데이터의 score

 

+)

데이터 생성을 모집단에서부터 sampling되는 것이라고 봤을 때, 모집단(MNIST)에서 sampling된 데이터들을 관측해서 분석을 진행하는 것.

• 모집단에서 sampling된 데이터 = 데이터 분포에서 높은 확률값을 갖는 위치에 있는 데이터
• 해당 데이터들이 높은 확률값을 갖기 때문에 sampling을 진행함에 있어서 자주 sampling이 되고 우리가 해당 데이터들을 관측하게 되는 것임

 

Score-based generative model의 기본적인 아이디어

간단한 score-based generative model

 

1. 데이터 공간 상에서 random한 noise 생성

2.  Score function(log PDF의 미분(gradient)) 계산

• 데이터 분포의 PDF를 알고 있다고 가정함! 
• score function은 데이터가 존재할 확률이 높은 방향을 가리킴

3. 초기 노이즈 상태에서 score function을 이용해 확률 값이 높아지는 방향으로 데이터를 점진적으로 업데이트 -> 데이터 포인트가 점점 실제 데이터 분포에서 높은 확률 밀도를 가지는 영역으로 이동함 

4. 업데이트 과정을 반복하면 초기 조이즈는 점차 샘플링된 데이터 와 유사한 데이터 생성 가능

• = random한 noise가 실제 데이터와 유사한 샘플로 변환됨 => 우리가 원하는 데이터를 생성하는 것이 가능해지는 것

 

Score matching for score estimation

Score matching : score function을 학습함으로써 실제 PDF를 구하는 것이 아닌, score 값을 활용해 PDF를 추정하는 것을 의미한다. 데이터 분포의 log 확률 밀도의 경사를 학습해 해당 분포를 모델링하는 방법이다. 

• 목표 : 주어진 데이터 x에 대한 score 값을 계산해주는 모델(Score Network)을 만드는 것
• 원리 : 데이터 분포의 score 함수와 모델의 score 함수를 일치시키는 것

 

증명

score matching은 다음과 같은 목표함수를 최소화하여 달성된다.

Score matching을 사용하면 먼저 p_data(x)를 추정하는 모델을 훈련하지 않고도 score network s_θ(x)를 직접 훈련해 ∇x log p_data(x)를 추정할 수 있다. 

아래의 식에서 true data distribution의 score function(빨간색)과 estimate한 score function(파란색)간의 fisher divergence를 최소화해야 한다. (min Loss가 목표)

• fisher divergence : 두 확률 밀도 함수 p(x)와 q(x) 사이의 차이를 측정하는 방법

score matching의 목표 함수(loss)

 

하지만 실제 data distribution(빨간색)을 알지 못하기 때문에 직접적으로 위 함수를 최소화하는 것은 불가능하다.

그래서 대신 부분 적분을 활용한 대리 손실 함수를 사용해 score matching을 진행한다.

대리 손실 함수 사용한 버

 

하지만 trace를 계산하는 과정에서 매우 큰 연산량이 요구된다는 단점이 존재한다.

• score matching의 objective에 있는 trace를 계산하고 학습을 진행하려면 항상 dimension의 개수만큼 backpropagation을 진행해야한다는 문제점이 존재함 (계산 복잡) → 이미지와 같이 높은 dimension을 지니는 데이터에 score matching을 적용하는 것이 현실적으로 불가능해짐
• 1024 X 1024 해상도의 이미지라면 총 1024번의 backpropagation을 수행해야 trace를 구할 수 있음

그래서 trace 연산을 효율적으로 수행하기 위한 방법으로 large scale score matching에 아래의 두 가지 방법을 사용한다. 

 

1. Denoising score matching

데이터 x를 입력받았을 때 x에 약간의 Gaussian noise를 추가한 x˜의 score를 예측한다. 

 

추가한 noise가 충분히 작으면 perturbated data distribution의 score가 원래 데이터의 score와 거의 같아서 원래 데이터의 score를 예측할 수 있다는 원리이다.

주어진 데이터의 분포에 대한 score를 직접 구하는 것이 아니라, 데이터에 주어진 noise에 대한 score를 구하는 것으로 문제를 변환한다. data point에 noise를 줘서 perturb(동요) 시키고 그 noise를 제거하는 방식으로 학습을 진행한다.

 

trace 부분을 대체하는데 아래의 distribution을 이용한다.

• 사전 정의된 noise distribution :

• noise perturbed data distribution :

  

→ 즉, 어떤 데이터 x가 주어졌을 때, 이것의 perturbed 데이터인 x˜의 분포를 학습하는 것

 

이때 위의 distribution을 바탕으로 objective function을 아래와 같이 수정해 모델을 학습할 수 있다.

 

즉, denoising score matching에서는 주어진 데이터의 분포에 대한 score를 직접 구하는 것이 아니라, 데이터에 주어진 noise에 대한 score를 구하는 것으로 문제를 변환하는 것!

 

2. Sliced score matching

random projection을 사용해 score matching의 tr(∇xsθ(x))의 근사치를 구한다. 

• p_v : 다변량 표준 정규분포와 같은 random vector의 simple distribution
• random projection의 과정: 무작위로 방향 벡터 v 선택 → 방향으로 projection 진행 → 그 point에 대해 score 계산

Denoising score matching과 달리 original의 unperturbed data distribution에 대한 score 추정값을 제공한다. 하지만 forward mode auto-differentiation으로 인해 4배 더 많은 계산을 필요로 한다. 

 

Sampling with Langevin dynamics - sampling

Langevin dynamics를 통해 score function log p_data(x)만을 사용해 PDF p(x)로부터 샘플을 생성할 수 있다. 

앞의 과정들을 통해 score network가 잘 학습되었다면 모든 데이터 공간 상에서의 score를 계산할 수 있는 것이다. 

• 이전 시점의 data에 score값을 더해 다음 시점의 data를 추정. 이때 local maximum 등을 벗어나기 위해 random noise를 더해준다.

임의의 데이터(random noise)에서 시작을 해서 score를 타고 올라가다 보면, 높은 확률값(샘플링 데이터와 유사한)의 데이터를 생성하는 것이 가능해진다. 

다음 x˜값을 update하는 과정을 반복함으로써 true data distribution을 따르는 샘플링이 가능해지는 것이다.

 

즉, p_data(x)에서 sample을 얻으려면 먼저 sθ(x) ≈ ∇x log pdata(x) 가 되도록 score network를 훈련한 다음 이 score function  sθ(x)을 사용해 Langevin dynamics로 샘플을 대략적으로 얻는 것이다. = score-based generative modeling의 framework의 핵심 아이디어

 

Chanllenges of score-based generative modeling

하지만 나이브한 score-based generative model은 몇 가지의 문제점이 존재하는데, 논문에서는 Manifold Hypothesis, inaccurate low data density data, slow mixing of Langevin dynamic 총 3가지를 지적하고 있다. 

 

1. The manifold hypothesis

: 실제 데이터 분포는 low dimensional manifold에 집중되는 경향이 있다고 주장하는 가설

• manifold : dataset을 잘 표현하는 subspace

 

이 가설에 의하면 SBGM은 아래 두 가지의 문제점을 갖게 된다. 

1. 데이터 x가 low dimensional manifold에 국한될 때 데이터의 score를 정의할 수 없다

• score는 ∇x log pdata(x) 이므로 gradient를 구할 수 없으니 정의가 불가능함

2. 데이터의 분포가 whole space일 경우에만 일관된 score estimate를 얻을 수 있다

• 본 논문에서는 Gaussian noise를 더함으로써 perturbated data distribution의 support를 whole space로 확장시켜 score matching이 일관되게 진행될 수 있도록 하였다. 

• Figure 1 (좌)은 ResNet을 CIFAR-10에서 sliced score matching을 통한 score 추정을 진행했을 때의 결과로, noise를주지 않고 score function을 학습할 때 manifold hypothesis 하에서 어려움을 겪는 것을 확인할 수 있다.
• (우) 에서는 약간의 Gaussian noise를 perturb줄 때 loss curve가 수렴하는 것을 보인다. 이는 Gaussian noise를 넣어줌으로 low demensional manifold에서 벗어나 perturbed data distributino이 온전히 R^D로 support 되기 때문이다. 

 

2. Inaccurate score estimation with score matching

: 자연 상태에서 가져온 데이터 분포가 우리가 알고자 하는 분포와 유사하다면, 실제 분포의 low density 영역의 data는 많이 없을 것이다.

즉, 데이터 분포가 sparse하기 때문에 특히 low density region에서 데이터의 희소성으로 score matching이 정확하게 이루어지지 않는 현상을 의미한다. (score function의 정확도가 낮아질 수 있다.)

 

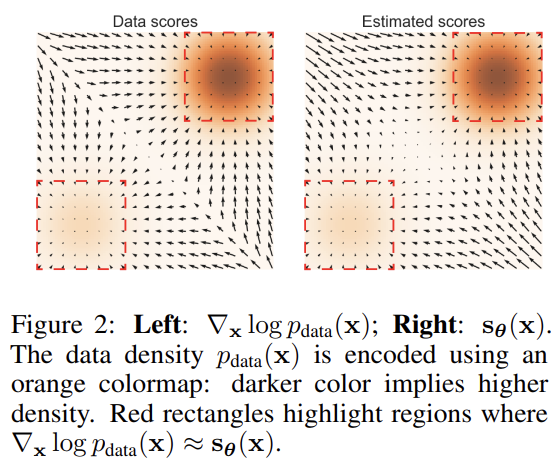
사진에서 데이터 분포에 대한 실제 score와 예측된 score(noise가 주어지지 않은 상태에서 학습한 모델이 예측한 score)가 다르게 나타남을 확인할 수 있다.

• 데이터가 주어진 부분(빨간색 점선) 내부의 예측은 정확하지만, 그 외 부분에 있어 오차가 발생한다.
• (좌)에 비해 (우)의 중앙을 보면, 데이터가 적은 부분의 score가 제대로 구해지지 않는 것을 볼 수 있다. 

이는 실제로 score function이 수렴하는지에 대한 이슈이며, sampling이 정상적으로 이루어지고 있는가에 대한 의문을 갖게 만든다. 

 

3. Slow mixing of Langevin dynamics

low density의 score는 또 다른 문제가 있는데, 만약 data distribution이 low density regions로 나뉘게 된다면 Langevin dynamics가 제대로 작동하지 않을 수 있다는 것이다. 

 

예로 아래와 같은 mixture distribution이 있다고 가정해보자. 

 

• π : data의 sampling을 결정하는 베르누이 분포 
• p1(x)와 p2(x)는 각각 정규화된 분포이며, 서로 다른 support를 가짐

 

 

• (a) : 실제의 iid sampling 결과
• (b) : Langevin dynamics를 사용할 때의 결과

 이는 score function의 방식 때문에 나타나는 차이로, 설명하면 다음과 같다. 

p1(x)의 support에서 p_data(x)는 아래와 같이 근사된다.

이 경우, score function은 다음과 같이 계산된다.

따라서 p1(x)의 support에서 score function은

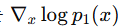
에 의존한다. 

마찬가지로, p2(x)의 support에서 score function은

에 의존한다. 

위의 두 경우 모두에서 스코어 함수 ∇x log p_data(x)는 π에 의존하지 않는다. 이는 이론적으로 π 값이 샘플링에 영향을 미치지 않는다는 것을 의미한다. 즉, 실제 분포와 상관없이 균일하게 sampling이 된다는 것이다.

⇒ Langevin dynamics는 결국 원본(a)과 정확하지 않은 것(b)을 생성하게 되는 것이다.

 

원래 데이터의 score인 ∇x log pdata(x)는 π에 의존하지 않기 때문에 MCMC sampling의 진행 과정에서 low density를 반영하지 못한다고 할 수 있다. 이론적으로는 수렴하게 하기 위해선 Langevin dynamics는 작은 step size와 많은 수의 step을 사용해야 한다고 한다. 

 

Noise Conditional Score Networks(NCSN): learning and inference

위 세 가지의 문제점을 극복하기 위해 논문에서는 perturbated data의 distribution을 이용하는 것이 score-based generative model에 적합하다고 결론을 내렸다.

• perturb시킬 때 위 논문에서는 gaussian noise를 사용함

 

그 이유로는 아래와 같다. 

1. Gaussian distribution은 whole space에서 정의되기 때문에, low demension manifold에 국한되지 않으며, 이는 manifold가설에 위배되지 않는다. 

• 가우시안 분포는 전체 공간에서 확률 밀도를 가지며 모든 방향으로 확산되어 있음. 이는 가우시안 분포가 저차원 구조에 국한되지 않음을 의미함.

2. Large noise가 unperturbated data distribution에서 low density region을 채우는 효과가 있어 더 향상된 score estimation이 가능하다. 

3. multiple noise level을 사용하여 실제 데이터 분포로 수렴할 수 있는 noise-perturbed distribution의 sequence를 얻을 수 있다. 

 

또한, simulated annealing과 annealed importance sampling의 정신으로 intermediate distribution을 활용해서 Langevin dynamics를 향상시킬 수 있다고 한다.

 

이러한 관점에서 논문의 저자는 아래의 두 가지 시도를 하였다. 

1. 다양한 레벨의 noise를 사용해 perturbated data를 만든다. 

2. single conditional score network로 모든 noise level에 대해 학습을 진행했다. 

 

이 두 목적을 이루기 위해 다음과 같은 score network, the training objective, annealing schedule for Langevin dynamic을 설명한다. 

 

Noise Conditional Score Networks

1. sigma scheduling

noise의 variance가 점점 커지는 형태로 이를 정의해서 이전 단계의 σ와 이후 단계의 σ비를 같게 설정하는 기하적 순열(=등비수열)(geometric sequence)를 이용했다.

 

시간에 따라 변화하지 않는 고정된 크기의 sigma(σ)를 사용하면 trade off 관계가 발생한다.

• noise(= σ)가 크면 low density region에서의 score가 잘 정의되지만, 실제 data distribution을 너무 많이 perturb해 정확도가 낮아진다는 단점을 가진다.
• 반대로 noise가 작으면 original data distribution에 비교적 작은 corruption을 할 수 있지만 sparse region에서의 score가 잘 정의되지 않아 오차가 발생하는 것이다. 

이러한 두 상황의 장점을 모두 취하기 위해 σ를 scheduling해서 변화시키며 넣어줘서 모든 noise level에 관해 학습을 진행하는 것이다. 기존의 Langevin dynamics로는 low density 부분을 accurate 할 수 없기에, data의 density의 σ(분산)를 키워서 low data density 부분에도 data가 존재하게끔 하는 것이다.

• low data density가 있을 때의 score function의 경우

 

• σ 를 키웠을 때의 score function의 경우 

 

 

그러나 σ 가 너무 크면 data의 정확한 density를 추정할 수 없으므로, σ 를 계속해서 바꿔주는 것이다.

이 σ를 계속해서 바꿔주는 이 방법을 annealed Langevin dynamics라고 하는 것이고, score function에 σ 를 조건부로 넣어주는 모델을 NCSN이라고 정의한다.

 

아래 그림에서 보이듯, σ가 작으면 low density를 잘 맞추지만, score function이 존재하지 않는 부분이 생기고, σ가 클 수록 모든 부분에 대해서 score function이 구해지는 것을 볼 수 있다. 이를 통해 NCSN 모델은 σ_large를 σ_small로 바꾸면서 sampling 결과를더 좋게 만드는 것이다. 

multiple scales of noise perturbations

 

하지만 이렇게 noise의 scale이 단계마다 다르면 각 단계마다의 obejective의 크기가 달라질 수 있다. 그렇기에 각 단계마다 적절한 weight를 가해서 objective를 더해줄 필요가 있다. 

 

즉, NCSN은 기존의 sθ​(x)에 대해서 조건부로 noise를 주는 것인데, 여기서의 noise를 σ로 정의하여 score function을 새롭게 정의한다.

기존의 데이터에 noise가 더해지는 방식

 

 

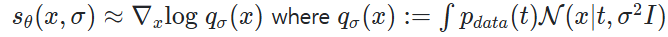
2. Training NCSN via score matching

score function의 학습은 score matching을 활용한다고 언급했는데, 본 논문에서는 denoising score matching 기법으로 score function을 학습시켰다.(sliced score matching도 작동함)

• 기존 score matching과의 차이점은 다수의 σ에 대응할 수 있도록 σ를 인자로 갖는 score function으로 정의하였다는 것이다. 

 

이때 noise distribution을 아래와 같이 정의한다. 

 

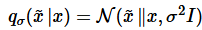
따라서 이때의 score function은 아래와 같이 정의할 수 있다. (가우시안의 미분)

 

즉 아까의 denoising score matching함수에 위 score function을 대입할 수 있다. 결론적으로 σ가 주어질 때 denoising score matching objective(loss function)는 아래(5)와 같다. 

이때 σ를 time step에 대해 정의하기 위해 최종적인 수식을 다음(6)과 같이 정의할 수 있다. 

 

• (5) : σ가 주어질 때 denoising score matching objective
• (6) : 모든 σ에 대해 합친 최종적인 objective

이때 λ 함수는 loss 값들의 크기 (Amplitude)를 균등하게 만들어주기 위하여 사용되었고, 주로 λ(σ)=σ^2으로 정의된다. 이는 score network가 실험적으로 1/ σ에 비례하기 때문에 이를 보정하기 위해서이다. 

이러한 사실까지 반영한 최종적인 수식은 아래와 같다. 

 

위 식은 아래와 같은 조건을 만족하기에  σ에 not dependent 하다고 한다.

 

 

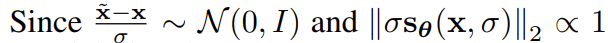
3. NCSN inference via annealed Langevin dynamics

NCSN을 통한 데이터의 생성은 다음과 같이 진행된다. L개의 서로 다른 sigma에 대해 내림차순으로 적용하여, 각 sigma에 대해 Langevin dynamics를 활용한 MCMC 과정을 진행하게 된다.

이때 업데이트 되는 정도 (η)와 noise의 크기를 별도로 정의된 step size를 활용한 식으로 바꾸어 "signal-to-noise" ratio를 유지할 수 있도록 하였다. 최종적인 inference algorithm은 아래와 같다.

 

 

이중 루프를 통해 sampling이 진행되는데 outer loop는 perturbation step의 총 step수인 L만큼, inner loop는 우리가 설정한 T step만큼 돌게되며 step size는 alpha_i로 설정이 된다.

 

Experiments

NCSN을 통해 이미지를 생성하면 GAN과 비슷한 성능의 높은 퀄리티의 이미지를 생성할 수 있다.

• 지금이야 GAN이 좀 오래된 모델로 여겨지지만, 당시 NCSN이 발표될 시점에서 GAN은 이미지 생성에서 성능이 가장 뛰어나다고 평가받고 있었기에 이러한 성능은 생성 모델계에서 괄목할 만한 성과였다고 할 수 있다.

 

---

[논문 리뷰]Generative Modeling by Estimating Gradients of the Data Distribution (velog.io)

[논문 리뷰]Generative Modeling by Estimating Gradients of the Data Distribution

[논문 Summary] NCSN (2019 NIPS) "Generative Modeling by Estimating Gradients of the data distribution" (tistory.com)

[논문 Summary] NCSN (2019 NIPS) "Generative Modeling by Estimating Gradients of the data distribution"

NCSN 설명 (Noise conditional score network 설명) - 유니의 공부 (tistory.com)

NCSN 설명 (Noise conditional score network 설명)

Generative Modeling by Es.. : 네이버블로그 (naver.com)

Generative Modeling by Estimating Gradients of the Data Distribution

Generative Modeling by Estimating Gradients of the Data Distribution (Noise Conditional Score Network) (glanceyes.com)

Generative Modeling by Estimating Gradients of the Data Distribution (Noise Conditional Score Network)

Score-based model에 대한 이해 (corelinesoft.com)